はじめに

電磁場のエネルギーについて考えてみる。

ジュール熱生成速度

媒質が真空で、電磁場中に置かれた電子について考える。
電子を一定の速度で$\Delta\boldsymbol{r}$動かすには
電子に外力$-e\boldsymbol{E}$加える必要がある。 f:id:shangtian:20181220233814p:plain

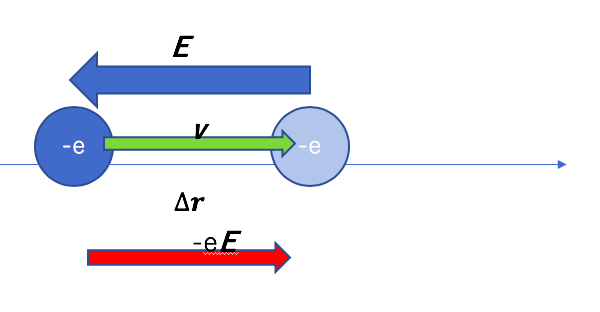
速度の向きを一定にするには磁場による
ローレンツ力を考慮しないといけないが電子の運動方向と
直交するのでエネルギーのやりとりは無い。

電子に与える仕事は $$ \Delta{W_e} = -e\boldsymbol{E}\cdot\Delta\boldsymbol{v} $$

電子が$\Delta{r}$移動するのにかかった時間を$\Delta{t}$とすると
単位時間あたり
$$ \frac{dW_e}{dt} = -e\boldsymbol{E}\cdot\frac{d\boldsymbol{r}}{dt} = -e\boldsymbol{E}\cdot\boldsymbol{v} $$ これだけ電子にエネルギーを加える必要がある。

電子密度をnとして単位時間・単位体積あたり電子に加えるにに
必要なエネルギーは

$$ \frac{dw}{dt} = -ne\boldsymbol{E}\cdot\boldsymbol{v} = - \boldsymbol{j}\cdot\boldsymbol{E} 　　　\cdot\cdot\cdot(1) $$

この電子が抵抗のある金属中を移動している場合は、
電子に加えたエネルギーはジュール熱として散逸してしまう。
よって$\boldsymbol{j}\cdot\boldsymbol{E}$はジュール熱の生成速度を表している。

今考えているのは真空中での電子の動きなので散逸は起こらない。

$\boldsymbol{j}$をマクスウェル方程式で消去する。

アンペール・マクスウェルの法則は $$ \nabla\times\boldsymbol{B} = \mu_0\boldsymbol{j} + \varepsilon_0\mu_0\frac{\partial}{\partial{t}}\boldsymbol{E} $$

なので、これを変形して

$$ \boldsymbol{j} = \frac{1}{\mu_0}\nabla\times\boldsymbol{B} - \varepsilon_0\frac{\partial}{\partial{t}}\boldsymbol{E} $$

これを(1)式に代入して $$ \frac{dw}{dt} = -\frac{1}{\mu_0}(\nabla\times\boldsymbol{B})\cdot\boldsymbol{E} + \varepsilon_0\frac{\partial\boldsymbol{E}}{\partial{t}}\cdot\boldsymbol{E} $$

これは単位時間・単位体積あたりのジュール熱を考えているんで、
体積Vの領域での単位時間あたりのエネルギーを考えてみる

$$ \begin{align} \frac{dW}{dt} &= \int \frac{dw}{dt}dV \\ &= -\frac{1}{\mu_0}\int(\nabla\times\boldsymbol{B})\cdot\boldsymbol{E}dV + \int\varepsilon_0\frac{\partial\boldsymbol{E}}{\partial{t}}\cdot\boldsymbol{E}dV \cdot\cdot\cdot(2) \end{align} $$

ここでベクトルの公式を使う $$ (\nabla\times\boldsymbol{B})\cdot\boldsymbol{E} = -\nabla\cdot(\boldsymbol{E}\times\boldsymbol{B}) + \boldsymbol{B}\cdot(\nabla\times\boldsymbol{E}) $$

(2)式の第一項を上の公式を使って整理して

$$ \begin{align} \int(\nabla\times\boldsymbol{B})\cdot\boldsymbol{E}dV &= -\int_V \nabla\cdot(\boldsymbol{E}\times\boldsymbol{B})dV + \int \boldsymbol{E}\cdot(\nabla\times\boldsymbol{E}) dv \\ &= -\int_{\partial{V}} (\boldsymbol{E}\times\boldsymbol{B})\cdot\boldsymbol{n} dS - \int\boldsymbol{B}\cdot\frac{\partial\boldsymbol{B}}{\partial{t}}dV \end{align}　\cdot\cdot\cdot(3) $$

(3)の第一項にはガウスの発散定理を用いて

$$
\int_{V} \nabla\cdot\boldsymbol{E}(\boldsymbol{r})dV = \int_S\boldsymbol{E}(\boldsymbol{r})\cdot\boldsymbol{n}(\boldsymbol{r}) dS
$$

(3)の第二項にはファラデーの電磁誘導の法則

$$ \nabla\times\boldsymbol{B} = - \frac{\partial\boldsymbol{B}}{\partial{t}} $$

を用いた。

(2)式に(3)式を代入して

$$ \frac{dW}{dt} = \int_{\partial{V}} \mu_0 (\boldsymbol{E}\times\boldsymbol{B})\cdot\boldsymbol{n} dS + \frac{d}{dt} \int_V(\frac{\varepsilon_0}{2}\boldsymbol{E}^2 + \frac{1}{2\mu_0}\boldsymbol{B}^2) dV $$

となる。第一項の面積分は考えている体積Vの領域の表面から単位時間に出て行くエネルギーを表し
第一項の被積分部分をポインティングベクトルと言って
$$ \boldsymbol{S} \equiv \frac{1}{\mu_0}\boldsymbol{E}\times\boldsymbol{B} $$ で表す。

第二項は電磁場のエネルギーの時間変化率を示している。よってエネルギー密度は $$ u = \frac{\varepsilon_0}{2}\boldsymbol{E}^2 + \frac{1}{2\mu_0}\boldsymbol{B}^2 $$

時間に依存する系であれば電磁場はエネルギーを持っていて無視できない。