ホール効果

はじめに

ホール効果について

前提

金属中に電流密度 \(\boldsymbol{j}\)の電流が\(x\)軸方向正向きで流れている。
また磁束密度\(\boldsymbol{B}\)で\(z\)軸方向正向きにかかっている。

図1 ホール効果

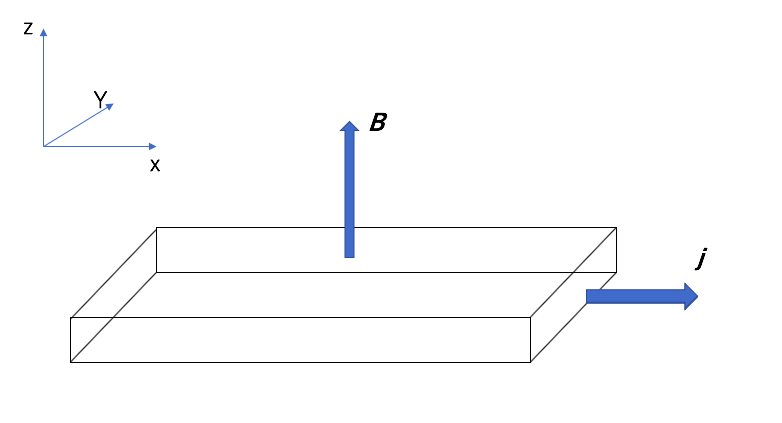
この時、電荷\(q\)のキャリヤーにローレンツ力が働く $$ \boldsymbol{F} = q\boldsymbol{v}\times\boldsymbol{B} $$

キャリヤーとは電子、正孔などの電荷をもつ粒子のこと。

図2 ローレンツ力を受ける

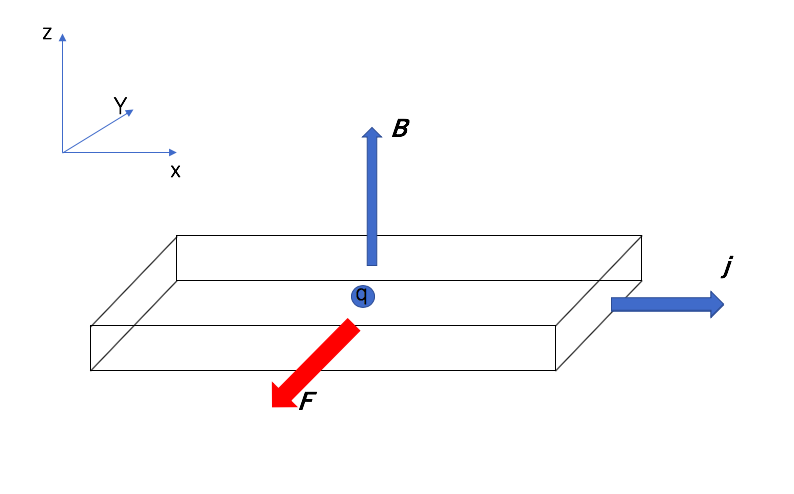
ローレンツ力を受けてキャリヤーに偏りが
生じてホール電場\(\boldsymbol{E_h}\)が\(\boldsymbol{y}\)軸方向に生じる。 $$ \boldsymbol{E_H} = R\boldsymbol{B}\times\boldsymbol{j} ・・・(0) $$

Rはホール係数である。

図３ホール電場

ホール係数を導く

電子を古典的な粒子として考えた時、電子の運動方程式は

$$ m^*\frac{d\boldsymbol{v}}{dt} = q\boldsymbol{E} + q\boldsymbol{v}\times\boldsymbol{B} - m^*\frac{v}{τ}　・・・(1) $$

\( - m^*\frac{v}{τ}\)の形で結晶内で電子が不純物や格子振動に衝突する影響を
摩擦抵抗の形で表している。また\(m^*\)は有効質量。

定常状態の時の様子を考える。x,y成分に分けて(1)の解を求めてみる。

$$ \frac{d\boldsymbol{v}}{dt} = \frac{q}{m^*}(\boldsymbol{E} + q\boldsymbol{v}\times\boldsymbol{B}) - \frac{v}{τ} \\ \frac{dv_x}{dt} = \frac{q}{m^*}(E_x + v_yB) -\frac{v_x}{τ} $$

今定常状態について考えているので\(\frac{dv}{dt} = 0\)である $$
m^*\frac{v_x}{τ} = q(E_x + v_yB)\\ v_x = \frac{qτ}{m^*}E_y + \frac{qB}{m^*}τv_y ・・・(2) $$

同様にしてy軸成分も考えると $$ v_y = \frac{qτ}{m^*}E_y - \frac{qB}{m^*}τv_x・・・(3) $$ となる。
(2)(3)式より\(v_x v_y\)を求める。この時電子の場合を考え
q=-eとし、\(\omega_c = \frac{eB}{m^*}\)とおいた。

$$ v_x = \frac{-\frac{eτ}{m^*}(E_x - (\omega_cτ)E_y)}{1 + {(\omega_cτ)}^2}\\ v_y = \frac{-\frac{eτ}{m^*}(E_y + (\omega_cτ)E_x)}{1 + {(\omega_cτ)}^2} $$

以上のように求まる。

単位体積あたりの電子数をnとすると、電流密度は
$$ \boldsymbol{j} = -ne\boldsymbol{v} $$

なので\(v_x v_y\)を代入して電流密度を求める。

$$ j_x = -nev_x = \frac{σ_0}{1+{(\omega_cτ)}^2}(E_x - (\omega_cτ)E_y) $$

$$ j_y = -nev_y = \frac{σ_0}{1+{(\omega_cτ)}^2}((\omega_cτ)E_x - E_y) $$

ホール効果の実験ではx軸方向のみ電流が流れるので\(j_y = 0\) となる
よってホール電場は $$ E_y = -\frac{eBτ}{m^*}E_x $$ 電気電動率は\(σ = \frac{n{e}^2τ}{m^*}\) これを(4)に代入して $$ j_x = σ_0E_x $$ 式(0)に代入し、ホール係数を求めると

$$ R = \frac{E_y}{Bj_x} = -\frac{1}{ne} $$

＜参考文献＞

固体物理学―工学のために